
Home |
Technical |
Up |
Next |
Prev |
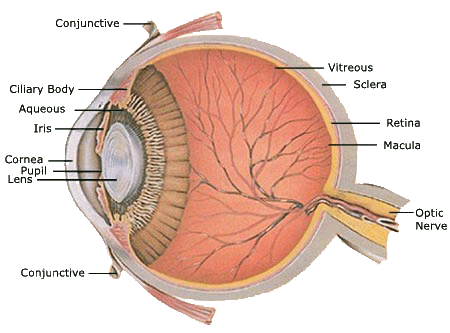
The Human Eye.
Human Brightness Perception
It is a fact that the eye discriminates intensity in a logarithmic fashion. This is unlike a semiconductor sensor, that discriminates in linear fashion. The eye's behaviour follows Stanley Smith Stevens' Power Law for human stimulus magnitude perception and varies as the cube rootfootnote 1. That is, that a human would subjectively rate actual intensities of 1, 8 and 27 as 1,2 and 3. Various people have quantified this, but the simplest is by Wyszecki in 1964: W = 25Y1/3 - 17 where W is the perceived brightness and Y is the actual brightness (both expressed in %). (the important thing here is that perception varies as the cube root, the other constants are just there to normalise the result to a 1 to 100 scale.)
If we set the sampling partitions in increments that vary as the cube then we will be storing the information that is most useful to the human observer. This information will need to be transformed later in various ways, and finally to appear on the display device in its original dynamic scale, but in the end, the eye will still discriminate brightness as the cube root, and thus the original info will be most efficiently transferred.
Compressing the photon count partitions in this way will also compensate for the effect of Poisson bloating at the high end, so lets see what happens when we use it!
Cubic Compression
Well, to cut a long story short, the cubic compression works a treat, improving discrimination greatly. Unfortunately, since the lowest level requires a mean photon count of at least 1, for a 12 bit dynamic range, the top level requires a mean photon count of at least 4,0963 = 6.9x1010 photons. Right out of the question. So let's compromise and use a square compression.
Square Compression
Again, assuming a minimum count of 1, a square compression requires a mean maximum photon count of 4,0962 = 1.7x107 photons. This is not out of the question for an SLR in good light, so at least we are at the gates of the ball park now.
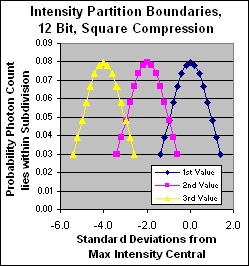
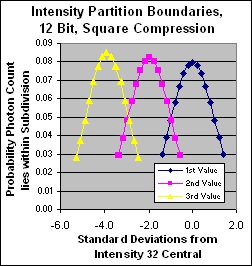
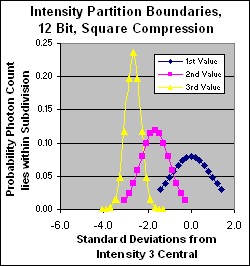
Partition discrimination in standard deviations for 12 bit dynamic range, square compression
Note that the partition discrimination under this compression regime is quite satisfactory, very steady across the range, and virtually identical to that of the uncompressed high end, yet we require only 1/4 the photons! Only at the bottom 2 levels is there any serious aliasing. A splendid result. Yes we have lost some linear discrimination but we humans don't need it. Cubic would suit us better but it's too big, so this is an excellent compromise.
Square compression really is the ideal! I tried using a power of 1.9 and it exhibited poor discrimination. Since most display devices and JPG files call for a gamma compression of 2.2 there are good grounds for using that instead of 2. It exhibits excellent discrimination but requires more photons.
OK so we have an effective 12 bit regime that is fine for SLRs in good light, but what about moderate or poor light? How can we shoot indoors?
Oh What A Lovely Fluke!
It just so happens that when you display an image on a CRT the intensity gamut of that image is expanded by the power of 2.2. This is purely a characteristic of those old phosphor coated vacuum tubes. In order to achieve the correct intensity gamut for the viewer the image must be compressed by the reverse amount before it is stored. In the video world this compression is called Gamma Correction and it has been around as long as television. The film world also has a Gamma but it is somewhat different. Almost everyone uses the sRGB standard which is roughly the power of 2.2. For the few devices that do not it is quite possible to convert between different Gammas (also known as Colour Spaces).
It is a lovely fluke that this compression is almost the ideal compromise between the ideal Poisson compression factor (power 2) and the natural responsiveness of the human eye (power 3)! Truly remarkable! This piece of serendipity is the reason so few people know about the necessity for Poisson square compression and the enormous effect of Poisson Aliasing. You don't need to know about it because you have already applied the cure by encoding all your video images with Gamma compression! Ironically, this is a compression applied for reasons that are no longer valid: ie we no longer use CRTs.
The Dynamic Range and Resolution Of The Human Eye
Although the human eye is capable of a contrast ratio of 1 or 2 million to 1, (about 20 stops), from midnight black to bright sunlit white, yet it takes the eye some time to adjust to these extremes. For the purposes of photography we are interested in its instantaneous dynamic range, about which there is some disagreement, but it is of the order of 1000:1footnote 2 (about 10 stops).
The human eye can detect just over 100 different brightness levels in the cubic domain. In order to convert a contrast step to a linear brightness value simply multiply the step number by 0.1 and cube the result. Step number 100 maps to (100*0.1)3 = 1,000.
* Note that although there is a linear step of 30 between levels 99 and 100, there is only a step of .001 between levels 0 and 1. To normalise the linear steps to a minimum of one we need to multiply by 1,000. As you would expect this gives a dynamic range of 1003 or 1 million in the linear domain. This means you need at least 1 million photons in the hot zone to fully satisfy the human eye. This is only one seventeenth of amount required under our 12 bit square compression regime (17 million photons)! Now we are in the ball park!!
* Note also, that although we now only require 100 levels, (or 6½ bits per colour per pixel), in the cubic domain, we are still sampling in the square domain (probably, or in the 2.2 domain more likely), so we still require 1,000 levels (or 10 bits per colour per pixel). This still equates to 1 million photons per hot pixel.
So, by dispensing with our dynamic reserves we have come down to a minimum of 1 million photons at the hot pixels. This is the limit however, if you are aiming for perfect results for humans. Any reduction in maximum photon count beyond this will result in either reduced dynamic range or some jaggedness in dynamic gradation visible to the best eyes under specific tests designed to reveal any dynamic shortfall. So have we got a working camera yet?
Well sort of... A refresh of the first table will show that 1 million photons per pixel will give us perfect results with an APS SLR under European office conditions or a Compact outdoors on an overcast day. But sadly folks, 1 million photons per pixel aren't available in a nocturnal lounge room, even with a 35mm SLR, much less a compact and we haven't even looked at limitations and inefficiencies in the hardware, which are substantial. So how can we take perfect indoor shots?
Well, sorry to disillusion you, but quite frankly: you can't! More on this later.
Display Contrast
Pictures mean nothing unless they are displayed, and this represents another place to shave a little, (or a lot), from the theoretical minimum resolution requirements.
We know that the human eye requires a contrast ratio of 1000:1 for full dynamic experience, so any display device capable of this should do the proper job and afford us no chance to cheat further, but the question of display contrast specs is a vexed one as one can discover by searching the net.
One has to be very careful of believing manufacturer's specifications, since it is in their interest to inflate their values to achieve greater sales, and recently those figures have gone through the roof! There are various ways to boost one's figures without completely lying so it is best to use the figures of a respected 3rd party. As of early 2009, typical contrast ratios from quality display devices were as follows:
- LCD monitors - 1,000:1
- Plasma monitor - 5,0000:1
- Printed page - 500:1
- Projected image - 500:1
As you can see, cinema and prints are less demanding, and we can reduce the required capture dynamic range to suit, however, computer and TV monitors offer no such out, their contrast ratio matches that of the human eye. We are stuck with our minimum of 1 million photons per hot pixel.
Your Monitor
As a matter of interest I include some test images to show how your monitor handles the contrast gamut. Firstly have a look at the 10 step strip. This goes from intensity 0 to 255 in steps of 10, (the last step is 16). On my monitor at least, the dynamic range is heightened in the centre of the range and lowered at the extremes. I am struggling to see a transition between the 2 darkest patches and can't make out the transition between the bright patches at all. This could be a limitation of my monitor, or it could be set up incorrectly (although I am very particular about my monitor setup), or perhaps it means that the gamma curve of the screen or the graphic application isn't quite matched to the human eye, probably deliberately so, since we are used to looking at mid-tone things.
If you can see 256 levels from black to bright green on your monitor, then not only is your monitor exceptional, but your eyes are super-human! 256 levels is what you get if you go up the green scale in steps of 1. I have provided a section of the 1 step strip from the middle of the range. Note however, what I have said above about dynamic range being heightened in the centre of the range and lowered at the extremes, so that even if you can make out the 1 steps, it doesn't necessarily mean you are really capable of 256 separate levels of green.

The entire display intensity spectrum of the green channel in steps of 10


A patch from the middle of a green strip in steps of 5 A patch from the middle of a green strip in steps of 3


A patch from the middle of a green strip in steps of 2 A patch from the middle of a green strip in steps of 1
Any More Bad News?
If you think things are bad so far I'm afraid it gets worse. But you've come this far, you might as well continue on with my discussion on
hardware limitations. By the time you finish that you'll be wondering how one can take a photo at all!
Here is the spreadsheet for this page's calculations.
- Wikipedia - http://en.wikipedia.org/wiki/Lightness_(color)
- Dynamic Range - http://dic.academic.ru/dic.nsf/enwiki/25974